Relatavistic Time and Lenght

Purpose:

            The object of both of these experimental activities is to gain a further and deeper understanding of the relativity aspect of length and time of object that are moving at speeds comparable to that of the speed of light. The online program of activity physics will be used to demonstrate how time and length changes with velocity of an object reaching speeds near that of the speed of light. Primarily, this lab will be dealing the equations of time dilution and length contraction.

Data analysis:

            Part 1: Relative Time

Question 1: Distance traveled by the light pulse
How does the distance traveled by the light pulse on the moving light clock compare to the distance traveled by the light pulse on the stationary light clock?

-          The distance traveled by the moving clock is further than the distance traveled by the stationary clock. 

Question 2: Time interval required for light pulse travel, as measured on the earth
Given that the speed of the light pulse is independent of the speed of the light clock, how does the time interval for the light pulse to travel to the top mirror and back on the moving light clock compare to on the stationary light clock?

-          Since the distance traveled is longer, the time required for the light to bounce off of the mirrors must be longer than for the stationary clock. 

Question 3: Time interval required for light pulse travel, as measured on the light clock
Imagine yourself riding on the light clock. In your frame of reference, does the light pulse travel a larger distance when the clock is moving, and hence require a larger time interval to complete a single round trip?

-          No, the time measured with the clock moving in the same frame takes the same amount of time. 

Question 4: The effect of velocity on time dilation
Will the difference in light pulse travel time between the earth's timers and the light clock's timers increase, decrease, or stay the same as the velocity of the light clock is decreased?

-          The difference will decrease as the velocity also decreases. 

Question 5: The time dilation formula
Using the time dilation formula, predict how long it will take for the light pulse to travel back and forth between mirrors, as measured by an earth-bound observer, when the light clock has a Lorentz factor (γ) of 1.2.

-          Using t=γt_o, the answer comes out to be: t = (1.2)(6.67) = 8.00s

Question 6: The time dilation formula, one more time
If the time interval between departure and return of the light pulse is measured to be 7.45 µs by an earth-bound observer, what is the Lorentz factor of the light clock as it moves relative to the earth?

-          t = t_0γ

γ = t/t₀ = (7.49)/(6.67) = 1.12

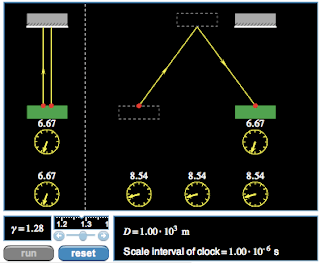
Part 2: Relativistic Length

Question 1: Round-trip time interval, as measured on the light clock
Imagine riding on the left end of the light clock. A pulse of light departs the left end, travels to the right end, reflects, and returns to the left end of the light clock. Does your measurement of this round-trip time interval depend on whether the light clock is moving or stationary relative to the earth?

-          No, it does not matter if the clock is moving and you are on it. 

Question 2: Round-trip time interval, as measured on the earth
Will the round-trip time interval for the light pulse as measured on the earth be longer, shorter, or the same as the time interval measured on the light clock?

-          Longer, since the light appears to travel a greater distance. 

Question 3: Why does the moving light clock shrink?
You have probably noticed that the length of the moving light clock is smaller than the length of the stationary light clock. Could the round-trip time interval as measured on the earth be equal to the product of the Lorentz factor and the proper time interval if the moving light clock were the same size as the stationary light clock?

-          The length has to be shorter so that the time difference factor, gamma, cane the same for both. 

Question 4: The length contraction formula
A light clock is 1000 m long when measured at rest. How long would earth-bound observer's measure the clock to be if it had a Lorentz factor of 1.3 relative to the earth?

-          l = l_o/γ = 1000/1.3 = 769m

Conclusion:

            For the first part of this experiment, we explored the properties of time when an object is traveling at comparable speeds to that of light. When an object is moving at such speeds, two different times are recorded, proper time, and diluted time. The proper time, as we learned, is the time interval in which is in the frame of that of the object moving. That is, when light has appeared to leave and return in the same spot. The diluted time is just the opposite. It is the time in which the light is emitted at one point and returns at another different from the original. This is called diluted time because it is not possible and would not make sense for there to be an instance in which there is contracted time.

            For the second part of the experiment, we explored the properties of length as speeds reach that close to light. The main factor learned is that the length is contracted whenever an object is moving at very fast speeds. Meaning that a stationary observer viewing an object moving at speeds comparable to the speed of light, sees the length of the object as shorter than what it is in actuality. This is called length contraction. The proper length, is the length that is measured from the frame that is moving. A person moving close to the speed of light in that reference is the same as the object, will measure the proper length.